Définition

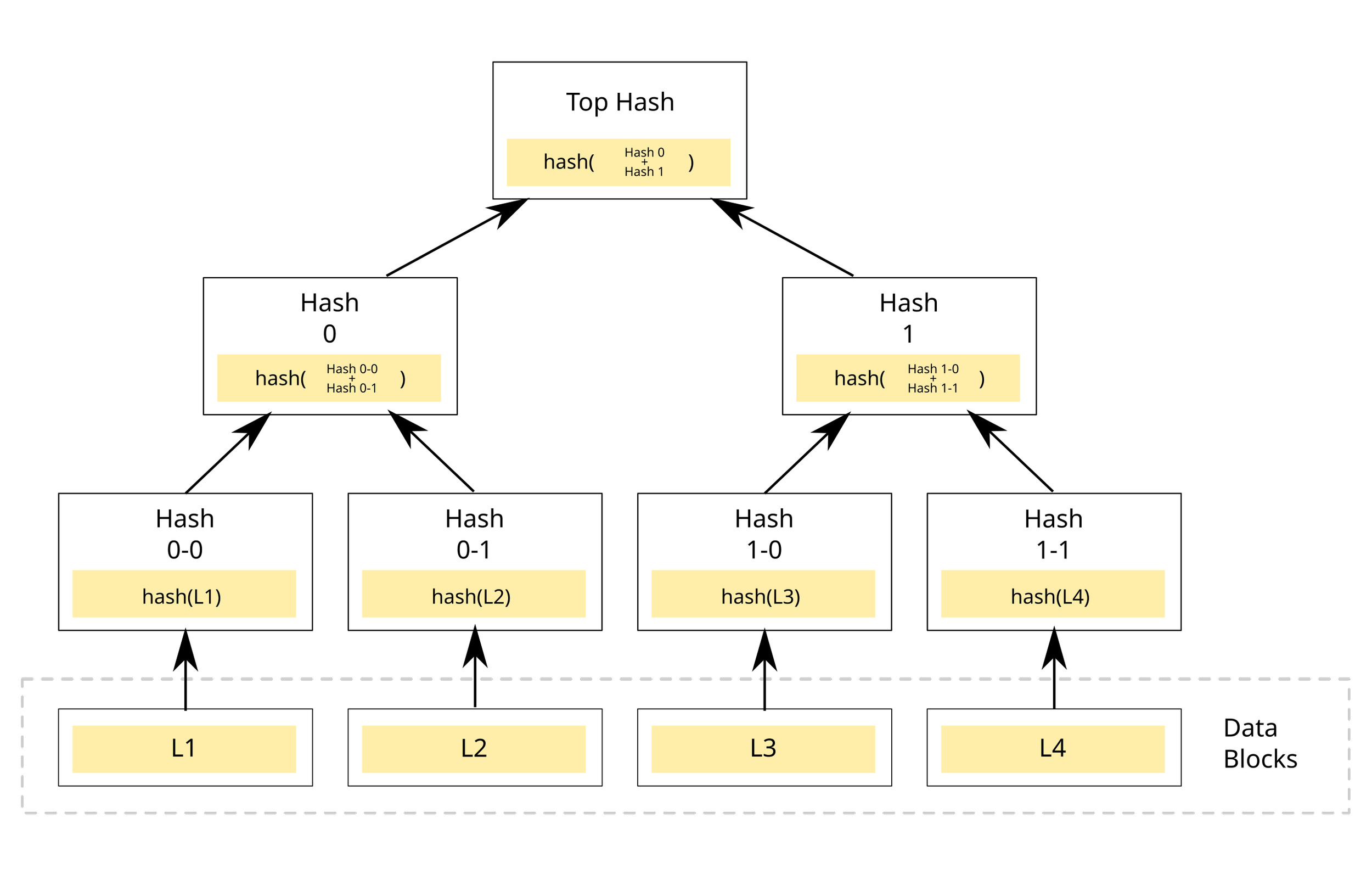
Un arbre de Merkle est une structure de données qui permet de vérifier qu’un élément donné appartient à un ensemble plus large en utilisant uniquement une petite portion de ces données. Pour construire cet arbre, on commence par prendre chaque élément brut, par exemple les quatre données représentées en bas de l’image ci-dessous : L1, L2, L3 et L4. Chacune de ces données est transformée par une fonction de hachage, c’est-à-dire une fonction cryptographique qui convertit une donnée en une courte empreinte numérique appelée hash. On obtient ainsi les hashs Hash 0-0, Hash 0-1, Hash 1-0 et Hash 1-1, chacun correspondant respectivement aux données L1, L2, L3 et L4.

Ces hashs de bas niveau sont ensuite regroupés deux à deux pour produire des hashs intermédiaires. Par exemple, dans l’image, Hash 0 est obtenu en combinant Hash 0-0 et Hash 0-1, tandis que Hash 1 est obtenu en combinant Hash 1-0 et Hash 1-1. Chaque hash intermédiaire résume donc l’ensemble des données qui se trouvent sous sa branche inférieure. Ce processus se poursuit jusqu’au sommet, où la combinaison de Hash 0 et Hash 1 produit un hash unique appelé ici Top Hash, plus couramment nommé racine de Merkle. Cette racine représente cryptographiquement l’ensemble complet des données allant de L1 à L4. A noter que si l’une de ces données était modifiée, la racine changerait immédiatement.

Preuve de Merkle (Merkle proof)

L’un des atouts fondamentaux d’un arbre de Merkle est la possibilité de produire une preuve de Merkle (Merkle proof). Cette preuve permet d’établir qu’une donnée, par exemple L3, appartient bien à l’ensemble global de l’arbre sans en révéler toutes les autres données. Pour cela, on fournit uniquement la donnée L3 et certains hashs intermédiaires nécessaires à la reconstitution du chemin menant jusqu’à la racine (Top Hash). Dans le cas de L3, il suffit de transmettre Hash 1-0 (le hash direct de L3), Hash 1-1 (le hash “frère” au même niveau), et Hash 0 (le hash du sous-arbre opposé). Avec ces seuls éléments, le vérificateur peut recalculer étape par étape les hashs intermédiaires, reconstruire la racine complète, et vérifier qu’elle correspond bien au Top Hash annoncé. Si c’est le cas, cela prouve que L3 figure bien dans l’ensemble {L1, L2, L3, L4} sans qu’il soit pour autant nécessaire de révéler toutes les données.

Cette construction permet donc d’assurer l’intégrité d’un ensemble de données tout en minimisant drastiquement la quantité d’informations à transmettre. C’est pourquoi les arbres de Merkle sont utilisés au cœur des chaînes de blocs en permettant de prouver l’existence ou la validité d’une donnée (par exemple une transaction ou une entrée de stockage) sans devoir télécharger l’ensemble du registre.

Utilisation des arbres de Merkle dans Bitcoin

Dans Bitcoin, les arbres de Merkle servent à organiser et à vérifier l’ensemble des transactions contenues dans chaque bloc. Chaque transaction est d’abord convertie en une empreinte cryptographique grâce à une fonction de hachage (SHA-256d). Ces empreintes constituent les feuilles de l’arbre, exactement comme les éléments L1, L2, L3 et L4 dans un schéma standard d’arbre de Merkle. Le protocole regroupe ensuite ces hashs deux par deux pour produire des hashs intermédiaires, de la même manière que Hash 0-0 et Hash 0-1 se combinent pour former Hash 0 dans un arbre classique. Ce processus est répété en remontant l’arbre jusqu’à obtenir un hash unique au sommet appelé la racine de Merkle (Merkle root). Cette racine résume cryptographiquement toutes les transactions du bloc. Elle est intégrée dans l’en-tête du bloc, aux côtés du hash du bloc précédent, du nonce et de l’horodatage.

Cette organisation permet ainsi à Bitcoin de vérifier efficacement l’intégrité de toutes les transactions d’un bloc à partir d’une seule valeur. Elle garantit qu’une modification, même minime, d’une transaction modifierait immédiatement la racine de Merkle, rendant la fraude détectable. Les arbres de Merkle constituent donc un élément structurel essentiel du protocole, en offrant une méthode compacte, sécurisée et efficace pour assurer la cohérence des blocs. Ils sont également utilisés dans certains mécanismes de vérification simplifiée du réseau, tels que ceux employés par les SPV nodes.

Conclusion

Un arbre de Merkle permet ainsi de représenter un ensemble de données de manière compacte tout en garantissant leur intégrité à partir de données sous-jacentes. En transformant chaque donnée en un hash, puis en regroupant ces hashs de manière hiérarchique jusqu’à une racine unique, la structure offre un moyen efficace de vérifier qu’un élément appartient bien à l’ensemble sans avoir à révéler toutes les autres données. Toute modification d’une seule donnée entraînerait une modification immédiate de la racine, ce qui rend la fraude détectable. Cette organisation en couches successives de hashs constitue donc un outil fondamental pour assurer la vérifiabilité, la sécurité et l'efficacité des systèmes distribués.